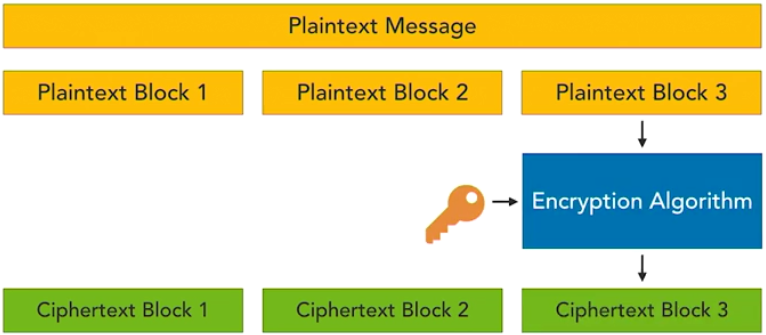
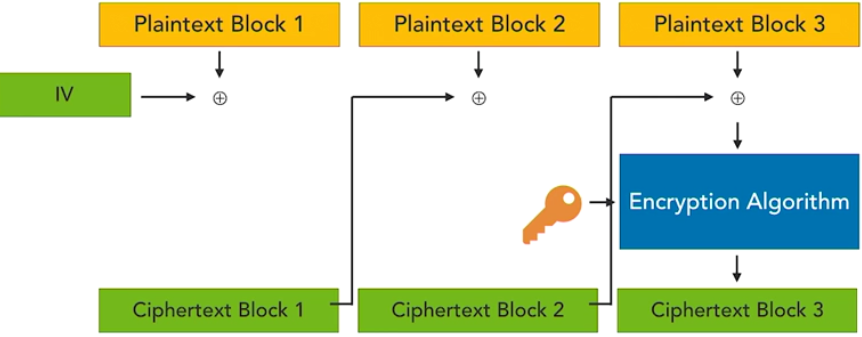
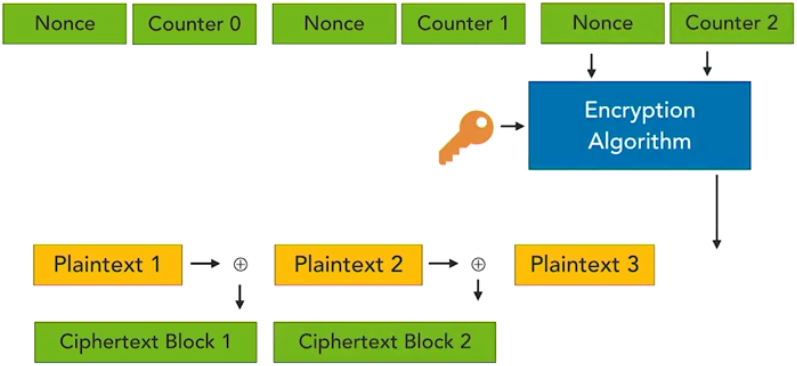
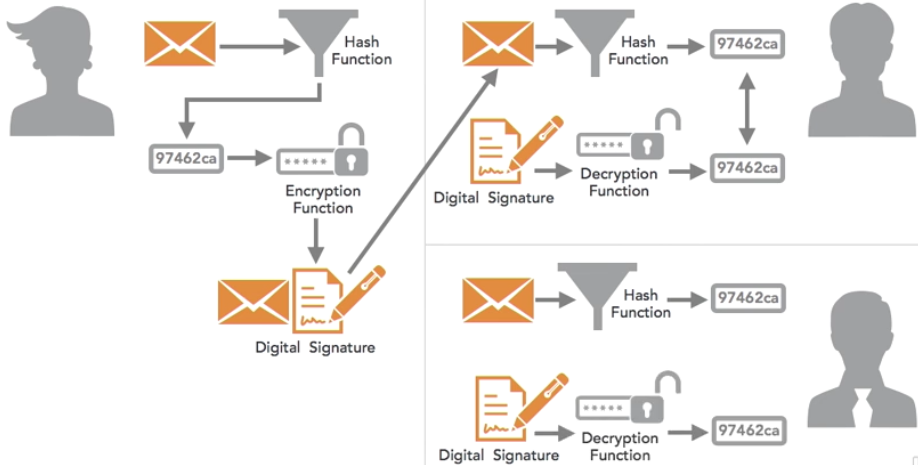
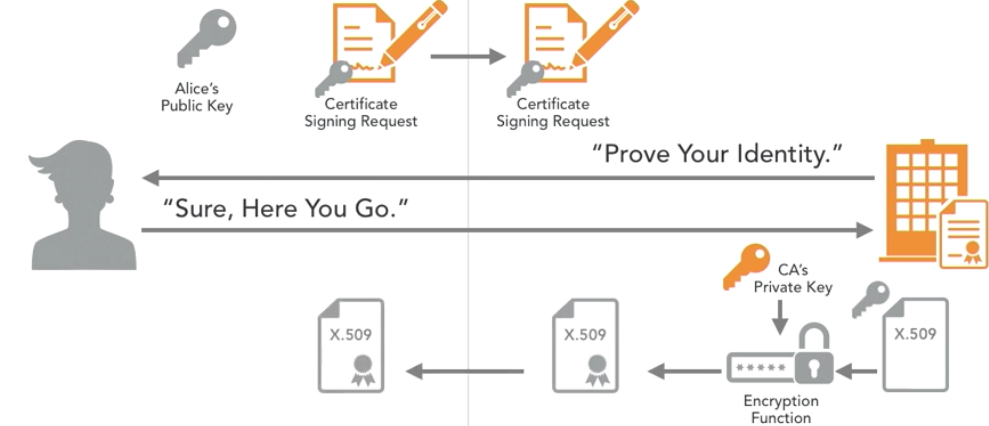
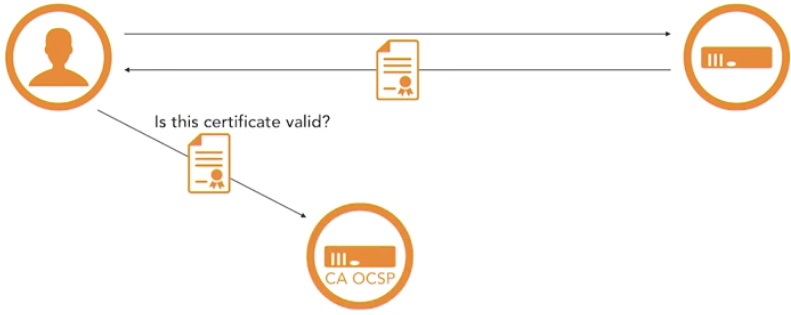
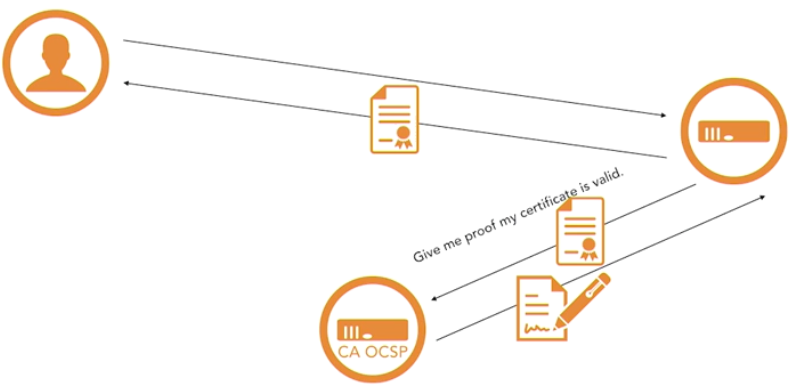
Here are some things you need to know for the Security+ examination.

Encryption

• Cryptography is the use of mathematical algorithms to transform information into a form that is not readable by unauthorized individuals (ciphertext). This relies on pseudorandom number generation because we lack a source of truly random numbers.
• Decryption performs the reverse transformation using an algorithm to transform that encrypted ciphertext back into plaintext format.
• Algorithms are processes or sets of rules to be followed in calculations or other problem-solving operations, especially by a computer. This is very similar to computer code and, in fact, computer code is often designed to implement mathematical algorithms.
• The encryption process uses two inputs, namely:
  • P = The plaintext message
  • K = The encryption/decryption key
  and the result of this process is C = The encrypted text
• The decryption process uses two inputs which do the reverse of the encryption process, namely:
  • C = The encrypted text
  • K = The encryption/decryption key
  and the result of this process is P = The plaintext message
• When sharing an encrypted message with someone, using symmetric encryption then K becomes the shared secret key which is used to encrypt and decrypt the message.
• Asymmetric encryption uses key pairs to process keys for secure communications, namely:
  • Public Key - Can be shared with other people
  • Private Key - Used only with the person creating the message
  Asymmetric communications is more scalable than symmetric communications, but is more processor intensive since asymmetric communications require the sender and recipient to use keys from the same pair. For example, if Bob wants to talk with Alice then Bob will use Alice's public key to communicate with Alice and then Alice will use her private key to decrypt the message. Since asymmetric communications is slow due to the requirements for more processor and memory resources, asymmetric communications is primarily used to distribute symmetric keys for faster secure communications.
• Symmetric encryption uses only shared keys for communications
• States of Data
  • Data at rest - Data on media (e.g. flash drive or hard drive) not being used at the moment
  • Data in motion - Data being transfered over a network connection
  • Data in use - Data that is in RAM and is being actively used at the moment
• The Cryptographic lifecycle has 5 parts, namely:
  1. Initiation - Gather requirements
  2. Development/Acquisition - Find an appropriate combination of hardware, software, and algorithms that meet objectives
  3. Implementation and Assessment - Configure and test
  4. Operations and Maintenance - Ensure the continued secure operation
  5. Sunset - Phase out the cryptographic algorithm

Formulas to determine the required number of keys to maintain secure communications:

• Symmetric Key formula: x = (n(n-1))/2 where n is the number of hosts and x is the number of keys needed for secure communications to everyone
• Asymmetric Key formula: x = 2n where n is the number of hosts and x is the number of keys needed for secure communications to everyone

Goals of Cryptography

• Confidentiality - Only authorized individuals can access information
• Integrity - No unauthorized changes
• Authentication - Proof of identity claims
• Nonrepudiation - Proving the origin of a message to a 3^rd party. This is only possible with asymmetric communications, using digital signatures.

Encryption Terminology

• Codes - Substituting one word with another to encrypt
• Ciphers - Using mathematical operations to encrypt - Ciphers have two different ways of processing a message, namely:
  • Stream Ciphers - Operate on one character, or bit, of a message at a time
  • Block Ciphers - Operate on large segments of the message at the same time
  Ciphers perform their encryption and decryption operations using two basic building blocks, namely:
  • Substitution Ciphers - actually change the characters of the message - For example, gratitude → kvexmxyi
  • Transposition Ciphers - rearrange the charaters on the message, but don't actually change them - For example, gratitude → trediguta
• ⊕ or Exclussive (XOR) - one input is different from the other input, namely:
  

  X	Y	X⊕Y
  FALSE	FALSE	FALSE
  TRUE	FALSE	TRUE
  FALSE	TRUE	TRUE
  TRUE	TRUE	FALSE

  
  Where X = the plain text input and Y = the encryption key For example, if X = gratitude and Y = encrypted then
  X⊕Y = 00000010 00011100 00010111 00011011 00001101 00000101 00010000 00001100*, using ASCII code for each letter in each word and then comparing their values.
  

  Word	ASCII code
  gratitude	01100111 01110010 01110100 01101001 01110100 01110101 01100100 01100101
  encryption	01100101 01101110 01100011 01110010 01111001 01110000 01110100 01101001 01101111 01101110
  * Binary	00000010 00011100 00010111 00011011 00001101 00000101 00010000 00001100

  *The result is given in binary since the resulting code of each character is not a letter in the English alphabet.

• Confusion - Every bit of the ciphertext must depend upon more than one bit of the encryption key.
• Diffusion - Changing a single bit of the plaintext should change about 50% of the ciphertext bits.
• Obfuscation - Uses cryptography to make the source code obscure, unclear, or unintelligible from unauthorized users.
• Steganography - The hiding of data in large files that produces slight modifications to the image pixels in a picture for the purpose of hiding messages in a way that only the intended recipient can read, using steganography software (e.g. QuickStego for Windows™ XP/7 [Free]). Steganography can use symmetric keys or asymmetric keys.

Encryption Algorithms:

Algorithm	Secure?	Symmetry	Comments
Rijndael algorithm or Advanced Encryption Standard (AES)	Yes	Symmetric	An encryption algorithm that Vincent Rijmen and Joan Daemen developed in January 2002 that is similar to the Data Encryption Standard, but uses 128-bit, 160-bit, 192-bit, 224-bit or 256-bit cipher blocks and is used in Wi-fi Protected Access version 2 (WPA2) communications
Data Encryption Standard (DES)	No	Symmetric	An algorithm developed by IBM in 1977 that uses the Horst Feistel function for 16 rounds of encryption, using 64-bit cipher blocks with a 56-bit key. This was based on the Lucifer algorithm. This was considered a secure encryption standard until December 2001.
Tripple DES (3DES)	Yes*	Symmetric	This a modified version of DES encryption algorithm algorithm that Walter Tuchman and his associates at IBM developed in 1999 that uses 3 rounds of DES (i.e. 64-bit cipher blocks) to encrypt plain text, using 3 different keys, using one of the following 3 options: K1 ≠ K2 ≠ K3 ≠ K1 - Effectively 168-bit encryption (best option) K1 ≠ K2 & K1 = K3 ∴ K2 ≠ K3 - Effectively 112-bit encryption (subject to the meet-in-the-middle attack ∴ no more secure than regular DES) K1 = K2 = K3 - Effectively 56-bit encryption (just as insecure as regular DES)
Lucifer algorithm	No	Symmetric	This was an encryption algorithm that Horst Feistel originally proposed on Tuesday, 01 May 1973, which used a 112-bit encryption key which became the basis for DES.
Blowfish (free)	No	Symmetric	This was developed by Bruce Scheier in 1993 as an alternate to DES that has the following characteristics: Uses a 64-bit block and variable key length from 32 bits to 448 bits Is free (no license required) Uses a Fiestel network Optimized for performance on 32-bit processors Combines substitution and transposition
Twofish (Free)	Yes	Symmetric	Developed by Bruce Scheier in 1998 as a replacement to DES which has the following characteristics: Uses a 128-bit block size Key sizes of 128 bits, 192 bits or 256 bits Uses a Fiestel network Combines substitution and transposition This was 1 of 5 finalists for the Advanced Encryption Security competition, but lost to the Rijndael algorithm which became the selected algorithm.
Ron's Cipher version 4 (RC4)	No	Symmetric	This is an encryption algorithm that Ron Rivest develped in 1987 as a trade secret, but was leaked to the public in 1994. This was one of the forerunners of RSA. This uses the XOR (⊕) function with a pseudorandom keystream on each character (byte) for encryption and decryption. The key length is variable from 40 bits to 2,048 bits. This was used with the following standards: Wired Equivalent Privacy (WEP) Wi-Fi Protected Access (WPA) - version 1 which uses Temporal Key Integrity Protocol (TKIP) for secure communications. Secure Socket Layer (SSL) Transport Layer Security (TLS) While there are no known instances of anyone breaking RC4, some experts found vulnerabilities in RC4 in 2015 ∴ RC4 is considered insecure.
RSA (variable length)	Yes	Asymmetric	Developed by Ron Rivest, Adi Shamir and Leonard M. Adleman in the 1970s that creates key pairs (public & private), using very large prime numbers and uses variable length keys from 1,024 bits and 4,096 bits. Therefore, RSA requires more computing power
Quantum Cryptography	Yes	Symmetric and Asymmetric	This employs quantum computing which is mostly theoretical that draws it strength from the weirdness or reality at small scales (≤ 100 μm) which results in Quantum Key Distribution (QKD) which uses a Quantum key that encodes and sends the information needed to decrypt a message in the fuzzy properties of particles, typically light particles. Therefore, it is not as susceptable as Elliptic Curve Cryptography (ECC) or RSA.
Elliptic Curve Cryptography (ECC)	Yes	Symmetric and Asymmetric	Uses the mathematical properties of elliptic curves to produce public key cryptographic systems. The following formula is used to draw the curve: y2 + axy + by = x3 + cx2 + dx + e  where a, b, c, d, and e, are real numbers.
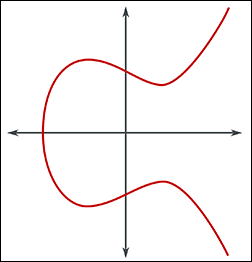Elliptic Curve Diffie-Hellman (ECDH)	Yes	Symmetric and Asymmetric	ECDH works the same way as Diffie-Hellman (DH) as shown below, except that it adds the functionality of ECC for more secure communications. A group number of 14 (2,048-bit) or greater is considered secure. Higher number group numbers combines the ECC algorithm with the Diffie-Hellman algorithm to create a more secure algorithm. The higher the group number, the higher the security.
Diffie-Hellman (DH)	Yes	Symmetric and Asymmetric	Developed in 1976 by Ralph C. Merkle, Bailey Whitfield Diffie and Martin Hellman as the first practical way of sending private messages by using a shared secret over an unsecured communication channel. Asymmetric encryption is used as a technique in key exchange mechanism to share secret key, but does not use prime factorization (see below for concept). After the key is shared between sender and receiver, the communication will take place using symmetric encryption. The shared secret key will be used to encrypt the communication. 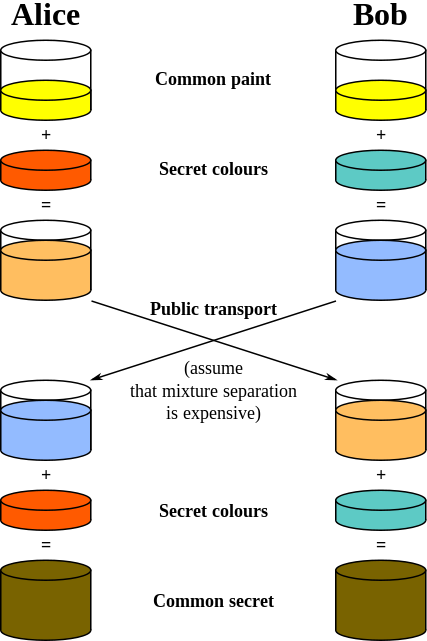The shared secret is the symmetric key that is used to encrypt the message.
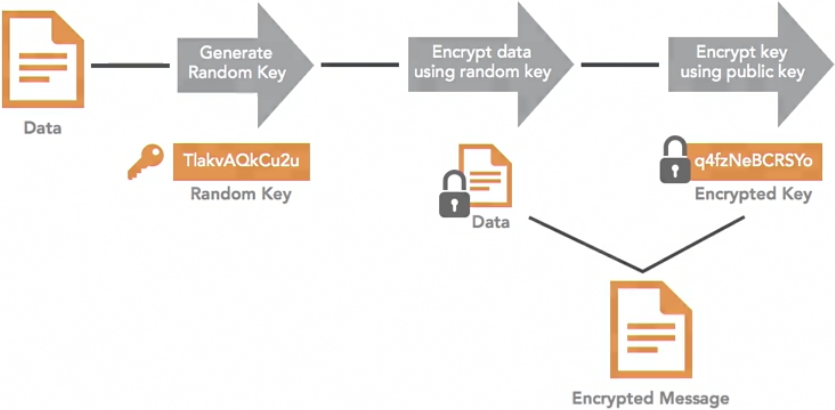
Pretty Good Privacy (PGP)+	No	Symmetric and Asymmetric	Developed by Phil Zimmerman in 1991 that goes through the following process to encrypt the message: Generates a random key Encrypts data, using a random key Encrypts the key, using a public key Produces the encrypted message with the encrypted data and encrypted public key. and goes through the following process to decrypt the message: Uses the private key to decrypt the original key and produce the encrypted data Uses the original key to decrypt the data. This relies on other encryption algorithms (e.g. RSA) to encrypt and decrypt the symmetric key the original message. 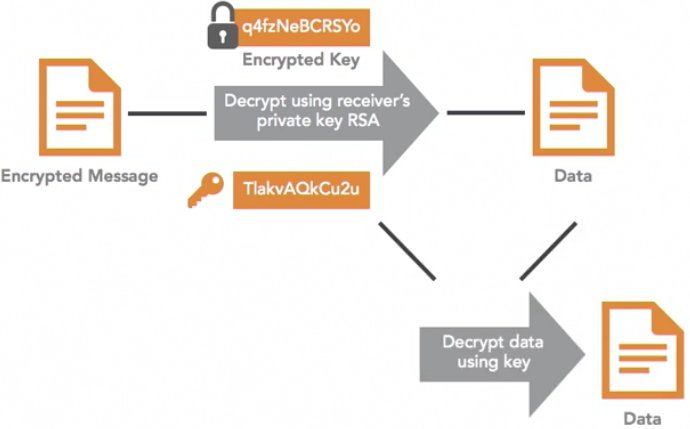There are commercial versions of PGP which are patented! There may be some versions that are secure, but for the most part, including the original version, are insecure.
GnuPG (GPG)+ also known as OpenGPG+	No	Symmetric and Asymmetric	This works the same way that PGP works and relies on other encryption algorithms (e.g. RSA) to encrypt and decrypt the symmetric key the original message, except that it is Open Source and Free (no patent).

Cipher Modes

• Electronic Code Book (ECB) Mode - contains the ciphertext image of each of some 8 character strings as a lookup table (see below).
  
• Cipher Block Chaining (CBC) - involves a vector bit sum operation of the message block with the previous ciphertext block prior to enciphering. The ciphertext blocks are initialized with a randomly chosen message which may be transmitted openly, i.e. the security of the cryptosystem is based on the secrecy of the key, not on the secrecy of initialization vector (see below).
  
• Cipher Feed Back mode (CFB) - allows one to process blocks of size r < n at a time. The typical value for r is 1, while n may be of size 64, using DES.
• Output Feed Back mode (OFB) - has a similar use as cipher feedback mode, but is relevant to applications for which error propagation must be avoided. Output feedback mode is an example of a synchronous stream cipher (constructed from a block cipher), in which the keystream is created independently of the plaintext stream.
• CounTeR mode (CTR) - Iterates by going from one plaintext block to another while using an encryption algorithm to combine a nonce with a counter and then do an ⊕ operation with the plain text to come up with the cipher text (see below)
  
• Galois/Counter Mode (GCM) - adds authentication capability and is constructed from an approved symmetric key block cipher with a block size of 128 bits, such as the Advanced Encryption Standard (AES). algorithm that is specified in Federal Information Processing Standard (FIPS) Pub. 197 [2]. Thus, GCM is a mode of operation of the AES algorithm.

Cryptography Concepts

• The Onion Router (Tor) - Provides anonymous web surfing
• Out-of-band - Exchange out of network communications
• In-band - Exchange over the network
• Key Escrow and Recovery or Encryption Key Escrow - Allows for Government backdoor for law enforcement; however, there is plenty of controversy on that (see New York Times article on Apple's reluctance to grant the FBI access to someone's data. for an example). Supported technologies include:
  • Clipper Chip (MYK-78) - A physical chip that allowed for Government backdoor for law enforcement which was mounted onto older motherboards
  • Recovery Agents such as Encryption File System (EFS) which allows somone else in an organization to recover a lost key.
• Key Stretching - Password-based algorithms which includes the following activities for strengthening, namely:
  • Salting - Adds a value to the encryption to make it more complex
  • Hashing - Add time to the verification process by requiring more math.
  This process should be repeated ≥ 4,000 times for good security. Meanwhile, here are a couple of common Key Stretching algorithms, namely:
  • Password Based Key Derivation Function version 2 (PBKDF2) - Applies a pseudorandom function to derive keys. The length of the derived key is essentially unbounded. However, the maximum effective search space for the derived key may be limited by the structure of the underlying pseudorandom function.
  • BCrypt - Uses a 128-bit salt and encrypts a 192-bit magic value and takes advantage of the expensive key setup in eksblowfish which is a variant of Blowfish, but goes through the encryption process 64 times using eksblowfish in ECB mode with the state from the previous phase. The output is the cost and 128-bit salt concatenated with the result of the encryption loop.
• Digital Rights Management (DRM) - Provides owners with technical means to prevent unauthorized copies (e.g. Apple Fair Play)
• Specialized Use Cases - Include the following technologies:
  • Solar power for satellite functionality
  • Radio Frequency IDentification (RFID) cards - A low power integrated circuit card that contains a unique identifier which can be read with an RFID scanner
  • Cipher chips that encrypt and decrypt data

Trust Models

• In person - A person physically shows up
• Web of Trust (WoT) - Relies on indirect relationships where participants digitally sign the public keys of the people they know personally. - Phil Zimmerman - Insecure and had the following issues:
  • Decentralized approach
  • High barrier to entry
  • Requires technical knowledge
• Public Key Infrastructure (PKI) - uses a Certificate Authority (CA) which is similar to getting ID from DMV

Hashing Functions (fixed length)

• Priciples only (not hashing function)
  • One way (→) functions (cannot reversed) used to verify data integrity
  • Output is same length regardless of the Input size
  • Each input to a hash function must be unique
  • Hash functions may fail if:
    • If they are reversible
    • If they are not collision resistant
  • Message digest is another term for hash.

Principles of Digital signatures

• Digital signatures use asymmetric cryptography to accomplish the following goals:
  • Integrity - Make sure the data remains unchanged
  • Authentication - Verify the source of the data
  • Non-repudiation - The assurance that someone cannot deny the validity of the data
• Digital signatures depend on a couple of things, namely:
  1. Collision-resistant hash functions (i.e. no two outputs are the same)
  2. Asymmetric cryptography (e.g. RSA)
• Digital signatures use private keys for encryption and public keys for decryption. This is reverse from when someone uses asymmetrical to send a private message, since that person (sender) would use a public key to encrypt a message and the recipient would use a private key to decrypt the message (see below).
  
  Note: Digitally signing messages does not provide confidentiality.
• Hash + Encryption = Digital Signature
• Digital Signature Standard (DSS) is the Federal Information Processing Standard (FIPS 186-4) that NIST's Computer Security Resource Center (CSRC) established on Friday, July 19, 2013 is a suite of algorithms that were issued by the National Information Standards and Technology that specifies the following three techniques for the generation and verification of digital signatures that can be used for the protection of data:
  • Digital Signature Algorithm (DSA) - Developed in 1991, and adopted as FIPS 186 in 1994.
  • Eccliptic Curve Digital Signature Algorithm (ECDSA) - The elliptic curve analogue of the Digital Signature Algorithm (ANSI X9.30 Part 1 [3]); see Annex G. The ECDSA shall be used in conjunction with the hash function SHA-1 defined in ANSI X9.30 Part 2 [4] which uses two related keys, a public key and a private key; the two keys have the property that, given the public key, it is computationally infeasible to derive the private key
  • Rivest, Shamir and Addleman (RSA) encryption algorithm - Please see above for description
• OpenSSL - Uses Rivest, Shamir, Adelman (RSA) and ECDS to generate a DSS
• X.509 - Invented by International Telecommuncation Union (ITU) to define frameworks for Public-Key Infrastructure (PKI) and Privilege Management Infrastructure (PMI). Please see https://www.itu.int/dms_pubrec/itu-t/rec/x/T-REC-X.509-201910-I!!SUM-HTM-E.htm for more information.

Digital Certificate Principles

• Digital certificates use the X.509 standard. Below is a diagram that shows the process of obtaining a valid digital certificate from an Certificate Authority (CA)
  
• Revoking Digital Certificates
  1. Certificate Revocation List (CRL) - CAs provide a list of the serial numbers of revoked certificates.
  2. Online Certificate Status Protocol (OCSP) - CAs provide a real-time service that allows users to verify that a certificate is not revoked. This is most popular since it is useful in determining the current revocation status of a digital certificate without requiring CRLs (see below)
     
  3. OCSP Certificate Stapling - extends OCSP's capabilities, but reduces the CA's burden (see below).
     

Digital Certificate Validation Principles

• We must pay fee to a Certificate Authority (CA) to obtain a trusted certificate
• Self-Signed Certificates (issued by an internal CA) are often used on intranets
• Certificate chaining allows the use of intermediate CAs - where an internal CA is validated by a 3rd party CA.
• Offline CAs protect sensitive root keys, but are typically used occasionally (brought online briefly) to validate intermediate CAs. This precerves the original keys.
• The Certificate Subject owns the public key - Vouches that the public key belongs to the owner.
• Keychain Access lists different root CAs
• A certificate Object IDentifier (OID) identifies unique object attributes (e.g. serial number) in a digital certificate. OIDs can help users trace the origins of a digital certificate.
• Certificate Subjects - Used in servers, devices and individual names and email addresses to associate a public key with an entity
• Certificate Pinning ties a certificate to a subject for a period of time.

Certificate Types

• Root - Protect CA private keys
• Wild Card (only one level allowed) - Match an entire domain (e.g. *.linkedin.com) and are commonly used for load balancers.

Verification Types

1. Domain Validation (DV) - Verify Domain Ownership
2. Organizational Validation (OV) - Verify Business Name
3. Extended Validation (EV) - Highest level that is often idicated by the name of the certificate holder in green next to the lock icon on a web browser. - This level of validation requires extensive investigation.

Certificate Formats

• Distinguished Encoding Rules (DER) - Specifies rule sets that govern how data structures that are being sent between computers are encoded and decoded. They come with following attributes:
  • Binary format
  • Use .der, .crt and .cer file extensions.
• Personal Information Exhange (PFX) or PKCS#12 files contain valid electronic signatures and come with the following attributes:
  • Binary format
  • Commonly used by Windows systems
  • Use .pfx and .p12 file extensions
• P7B or PKCS#7 files are earlier versions of PFX files that come with 64-bit encryption and have the following attributes:
  • ASCII text equivalent of PFX certificates
  • Commonly used by Windows systems
  • Use .p7b file extension
• Privacy Enhanced Mail (PEM) - An older certificate standard which is not used very often today, but still provides for secure exchange of electronic mail. They come with the following attributes:
  • ASCII text equivalents of DER certificates
  • Convert with OpenSSL
  • Use .pem and .crt file extensions
  Note: CRT files may be either DER binary certificates or PEM text certificates.

Other Cryptography Principles

• Networked Cryptography requires low latency
• High resiliency requires the protection o encryted data

Type of Attacks:

1. Brute-force - Known as ciphertext attacks which involves guessing the password or its hash value to gain unauthorized access. For example, dictionary attacks are a form of brute-force attacks.
2. key space Attacks - Use the set of all possible encryption keys that are usable with an algorithm.
3. Knowledge-Based - requires knowledge of something
   • Frequency Analysis - Study of patterns
   • Known Plain - Text Attack
   • Chosen Plain - Text Attack

There is more information on certmike.com or you can send an email to Mike Chapple if you still have any questions about this content.

The navigation options for this page are:

• Go back to Domain #5 → Risk Management,
• Return to the main Security+ resources page,
• Return to the main Nine Star training website, or
• Go to the main Nine Star website.